What are Circle Theorems? A guide with examples
What are circle theorems?
Circle theorems describe the relationships between angles in a circle. For the purposes of most maths exams, you can assume that the circles theorems are true and state them in your answers, unless the question explicitly asks you to prove them. Proving circle theorems will be covered further down.
What circle theorems are needed for GCSE?
There are seven main circle theorems which you need to memorise for your GCSEs. They are:
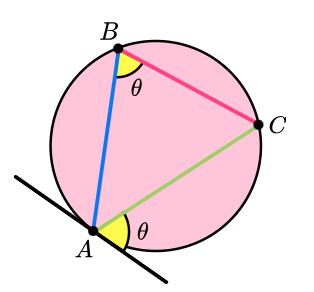
1. Alternate segment theorem - the angle between a chord and a tangent is equal to the angle in the other segment of the circle.
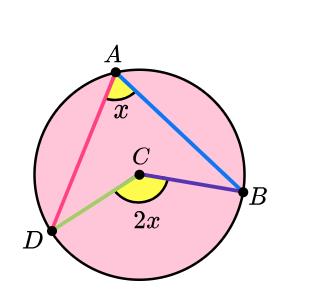
2. The angle at the centre of the circle is double the angle at the circumference
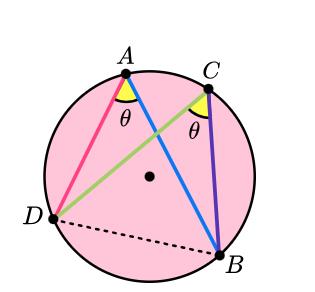
3. Angles in the same segment are equal
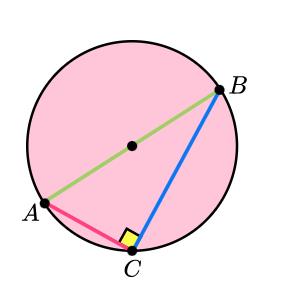
4. The angle in the semicircle is 90 degrees
5. The radius which is perpendicular to a chord splits the chord into two sections of equal length (bisects the chord)
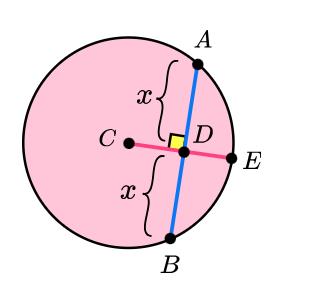
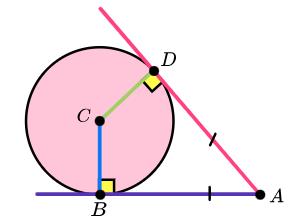
6. The angle between a tangent and a radius is 90 degrees, and tangents which meet at a point are equal in length (i.e. in this diagram the lines AB and AD have the same length)
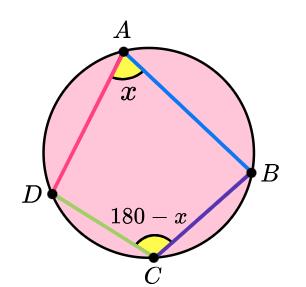
7. Opposite angles in a cyclic quadrilateral add up to 180 degrees
When to use circle theorems
Whenever you get a question which includes a diagram of a circle and asks you to find an angle, there's a good chance you're going to need to use some circle theorems to solve it. There are a few general pieces of advice which you should bear in mind when answering those questions.
-
Start by listing all of the circle theorems which could be relevant to the question.
-
Remember to explain every step of your working - including listing any circle theorems and other results which you use.
-
You may need to use techniques from other topics as well as circle theorems - for example you will often need to use results about triangles, quadrilaterals and so on to answer the question.
Example question
Have a go at the question below, then check the example solutions underneath to see how you did.
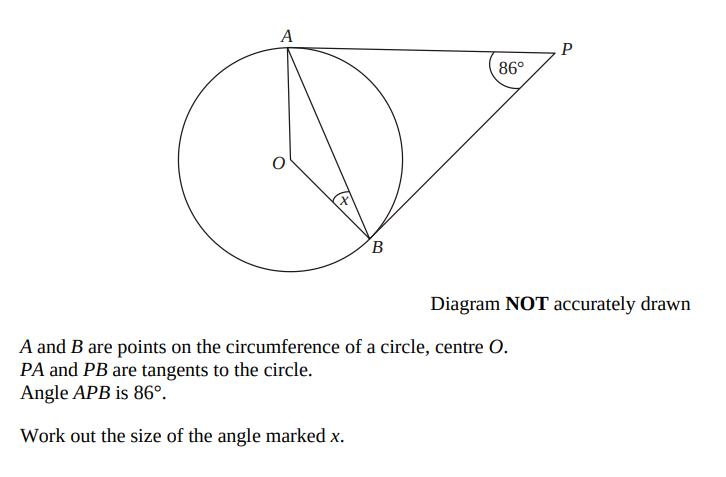
Solution
Since two tangents which meet at a point have equal length, we know that AP is equal to AB, which makes triangle ABP isosceles.
This means angle PAB is equal to angle ABP, and since angle APB = 86 degrees, and the angles in a triangle sum to 180 degrees, then PAB = ABP = (180 - 86)/2 = 47 degrees.
The angle between a tangent and a radius is 90 degrees, which means that angle OBP is equal to 90 degrees.
Therefore x = 90 - 47 = 43 degrees.

Alternative solution
Since the angle between a radius and a tangent is 90 degrees, angle OAP = angle OBP = 90 degrees.
The angles in a quadrilateral sum to 360 degrees, so angle AOB = 360 - (90 + 90 +86) = 94 degrees.
Triangle AOB is isosceles with OA = OB since OA and OB are radii of the circle. This means angle OAB equals angle OBA, and since the angles in a triangle sum to 180 degrees, x = (180-94)/2 = 43 degrees.
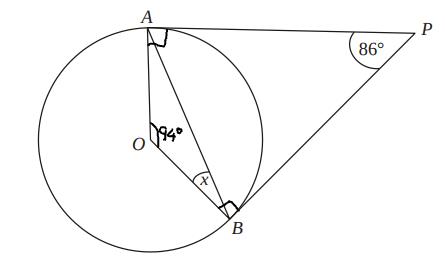
Both of these methods give the correct solution, so they would both be valid in an exam.
Proofs of circle theorems
Sometimes GCSEs will include a question asking you to prove one of the circle theorems. The proofs which you may get asked about are outlined below.
Proof that the angle at the centre of the circle is double the angle at the circumference
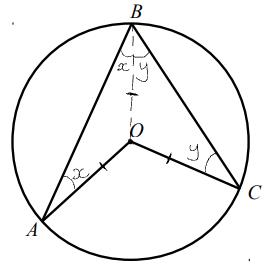
The proof starts by adding in the line OB to create two triangles. These triangles are both isosceles since OA, OB and OC are all radii so have the same length.
This means that angle OAB = angle OBA (which we can label x) and angle OCB = angle OBC (labelled y)
Then angle AOB = 180 - 2x and angle COB = 180 - 2y so the reflex angle AOC = 180 - 2x + 180 - 2y = 360 - 2x - 2y. This means the non-reflex angle AOC = 360 - (360 - 2x - 2y) = 2x + 2y.
Angle ABC = x + y, so angle AOC is double angle ABC.
Proof that angles in the same segment are equal
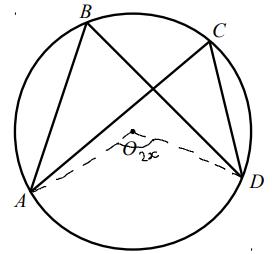
We can add lines AO and AD to the diagram to create angle AOD, labelled 2x. We can then use the previous circle theorem, which says the angle at the centre is twice the angle at the circumference. This means that angle ABD = x and angle ACD = x. Therefore angle ABD = angle ACD.
Proof that the angle in the semicircle is 90 degrees
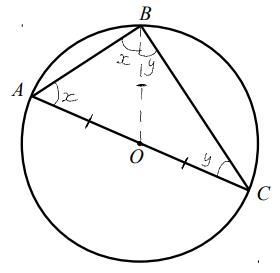
Again, we start by splitting the triangle into two smaller triangles by adding the line OB. We know that OA = OB = OC since they are all radii, so angle OAB = angle OBA (labelled x) and angle OCB = angle OBC (labelled y).
This means angle AOB = 180 - 2x and BOC = 180 - 2y, so angle AOC is 360 - 2(x + y). However AOC is a straight line, so angle AOC = 180 degrees. Therefore 360 - 2(x + y) = 180, which can be solved to show that x + y = 90 degrees.
Angle ABC = x + y so angle ABC = 90 degrees.
Proof that opposite angles in a cyclic quadrilateral sum to 180 degrees
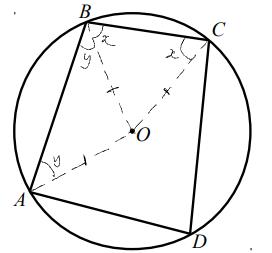
We can add in the radii AO, BO and CO, which means angle OBC = angle OCB = x and angle OAB = angle OBA = y.
Then angle AOB = 180 - 2y and angle BOC = 180 - 2x, so angle AOC = 360 - 2x - 2y.
Since the angle at the centre of the circle is double the angle at the circumference, angle ADC = (360 - 2x - 2y)/2 = 180 - x - y.
Therefore angle ABC + angle ADC = x + y + 180 - x - y = 180 degrees.
Proof of the alternate segment theorem

We start by drawing a diameter of the circle which passes through C, and label the other point where it touches the circumference F. Then angle FBC is a right angle, since the angle in the semicircle is a right angle.
Then we call angle BCE x. Since the angle between the radius and the tangent is 90 degrees, angle ECF = 90 degrees so angle BCF = 90 - x.
Therefore angle CFB = 180 - 90 - (90 - x) = x.
Since angles in the same segment are equal, angle CAB = x. Therefore the angle between the chord and the tangent is equal to the angle in the opposite segment.
I hope this article has helped you understand what circle theorems are and how to apply them to exam questions. If you still have any questions, feel free to get in touch with me!


