What do quadratic equations, canon balls and cricket matches have in common?
Cricket balls, Cannonballs, Curves...
As a kid, I used to spend countless hours playing cricket in the grassy fields of Nepal. Though I made sure to hurl the cricket balls as fast as possible to my opponents, they always hit the ball dead centre! How effortlessly they swung the bat hitting the ball over my neighbour's fence! One cannot stop and appreciate such a perfect shot where the balls glide elegantly through the air tracing a beautiful arc!
But what could this exact shape be? What are their exact features? Have you ever wondered about that? Whatever you hurl in the air at an angle, whether it be a cricket ball or a cannonball, travels through the air tracing this specific shape.
Well, that my friends, is a shape traced traced out by a quadratic equation! I never guessed that I was seeing the same quadratic equations from the textbooks for maths lessons in the cricket fields, but that is perhaps the beauty of paying attention.
Defining Quadratics
Let's dive into really understanding what the quadratic equation is now.
The quadratic is a member of the family of the polynomial curves. Well, what are polynomials then?
Polynomials are algebraic expressions that only have a variable like 'x' raised to some numerical exponent plus a number/constant (this number/constant can be 0 too!). Below are some polynomials:

Notice how we only have expressions with 'x' raised to some exponent plus a number/constant (the last example has a constant of 0). Let me give you an example of what is not a polynomial.
![]()
Yes, 3 raised to the x is not a polynomial because a polynomial must have a variable base (like 'x') and a numerical exponent (exponent which is a number and not a variable).
So, what exactly is a quadratic then? Well, quadratic is that member of the polynomial where the highest power of the variable (in our case 'x') is 2. Below are a few examples of quadratic:

Notice how all the expressions have an x-squared term and no term with an exponent greater than the x-squared term (meaning that expressions with terms like x-cubed aren't quadratics).
So, a quadratic expression has two properties:
1. Must have an x-squared term.
2. Must not have any term that has a greater exponent than x-squared.
Below is an expression that is not a quadratic:
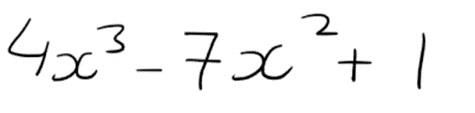
This expression is cubic and not quadratic because the highest power of the variable 'x' is 3.
So, quadratic expressions are those that have the highest power of the variable 'x' being equal to 2.
Now, quadratic equations are those equations which can be simplified and written as a quadratic expression being equated to 0.
Here's an example:

Let me ask you a question now. Is the following equation quadratic?
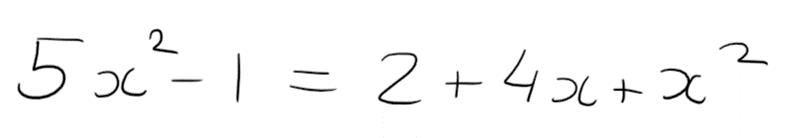
A first glance might get you thinking that it's not a quadratic because we don't have a quadratic expression equated to 0 BUT remember that an equation is quadratic if it can be simplified and written as a quadratic expression being equated to 0. We can simplify this equation by subtracting x-squared, 4x and 2 from both sides of the equation like this:
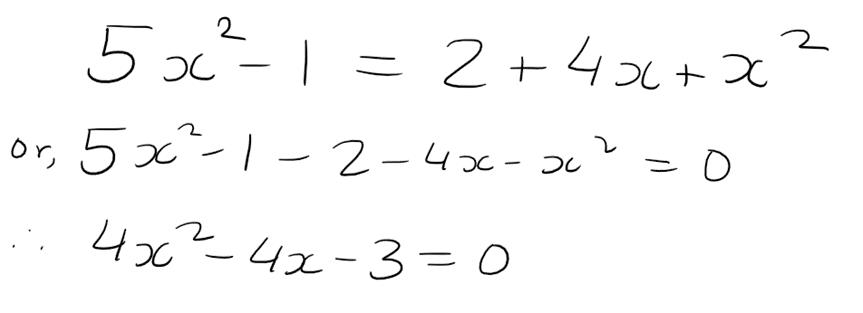
So, to get around this simplifying business, we can define the quadratic equation as any equation of the form:
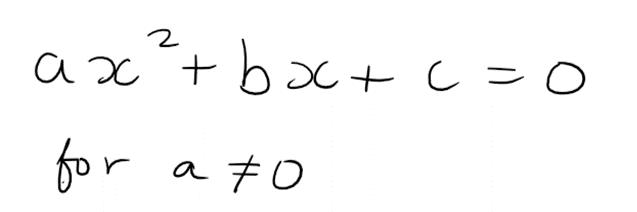
Where a,b,c are any numbers. Note that we impose that a is NOT equal to 0 because if a = 0 then the expression would no longer be a quadratic.


