How to Solve Quadratic Equations in the Simplest Way
Maths is a subject that often leads to the highest rates of school failure, the one where most students tend to fail, and the one that demands the most private maths tutors. So, if you're struggling, don’t worry, you’re not alone. We're here to help you pass your maths exams with these tips for solving equations.
Find GCSE Maths Private Tuition
Equations are undoubtedly one of the most challenging parts of this subject to understand. They often require the most time during compulsory education and are fundamental if you want to pass maths and continue your studies.
The most important thing about equations is understanding them and being able to reproduce what you’ve learned. Mastering them takes time, so don’t get frustrated. We'll explain how to solve a quadratic equation, but you can always find a maths tutor who can help you understand them in just a few intensive lessons.
What Are Quadratic Equations?
Equations are mathematical equalities where we don’t know one of the terms or numbers that form the equality. When we refer to quadratic equations, it means that the unknown (called the variable) is raised to the power of two, which means it’s multiplied by itself.
There are three types of quadratic equations, each with its own way of being solved:
- Complete quadratic equations
- Incomplete quadratic equations with the absence of B
- Incomplete quadratic equations with the absence of C
But what does the absence of B or C mean? First, we need to understand what a complete equation is, and then the rest will make sense.

How to Solve Complete Quadratic Equations
First, we need to fully understand what a complete quadratic equation is. All these equations have the following structure:
x²+ x - 2 = 0
At first, you’ll always find equations presented this way, but if not, you’ll have to simplify them until they look like this. The first step is always to arrange all values on one side of the equation so that it equals 0.
Then, we apply the quadratic formula to solve the equation:
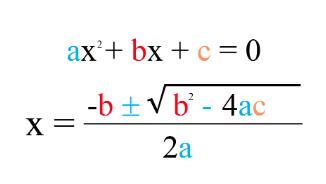
In order not to confuse X with the multiplication sign, we will represent these operations from now on with a “ · ”. But what do a, b and c mean in this formula? It is very simple:
- The letter a is the value that accompanies x².
- The letter b is a value that accompanies x.
- The letter c is a value that we know.
So in the previous example, A would be 1 (if there is no number accompanying the x, it is understood that it is 1), B would also be 1 and C would be the number 2. And we only have to substitute these values in the formula and solve it as if it were a first degree equation.
If we remember the order in which operations must be done, here’s how to proceed:
- Solve the exponent inside the square root.
- Solve the addition or subtraction inside the square root.
- Calculate the square root.
At this point, you might be wondering what it means to have a + sign and a - sign. This is because every quadratic equation has two solutions:
- First solution: perform the addition and solve the fraction.
- Second solution: perform the subtraction and solve the fraction.
There are some considerations to keep in mind to fully understand them:
- If, when solving the operations inside the square root, you get a negative number, the equation has no real solution. This is because the square root of a negative number does not exist.
- If, when solving the operations inside the square root, the result is 0, we have a double root because adding or subtracting 0 makes no difference.
Once we’ve mastered solving complete quadratic equations, we can move on to the incomplete ones.
How to Solve Incomplete Quadratic Equations When B is Missing
As we’ve seen before, missing the B term means the linear term (the x not raised to any power) is absent. If the linear term is present but has no value in front, it means its value is 1. This method is used when we only have x² and the constant term C.
Example:
x²-25=0
As we saw with complete equations, if the equation doesn’t follow this structure, we’ll need to simplify it until it does. Then, we can use the quadratic formula we saw earlier, but when substituting B, we’ll input 0.
There’s actually a much simpler way to solve these equations:
- Move the constant term to the other side of the equation. Example: x²−25=0 becomes x²=25
- Take the square root of both sides. Example: x=√25
- Solve, noting that the result will be both positive and negative. Example: x=+5 x=-5
Remember, if you encounter a negative square root, the solution doesn’t exist. If x² has any coefficient, divide by that value before taking the square root.
How to Solve Incomplete Quadratic Equations When C is Missing
This is the last type of quadratic equation, where the constant term c is missing, and we only have x² and x.
First, you need to understand polynomial factoring. If you’re unfamiliar with this topic, it’s a good idea to review it before continuing.
As with all quadratic equations, the first step is to simplify the equation until it has this structure:
x²-9x=0
Next, follow these steps:
- Find the common factor among the terms of the polynomial. Example: Here, the common factor is x, so the equation becomes x(x−9)=0
- The first solution is the value of x outside the parentheses, which is 0.
- The second solution comes from solving the equation inside the parentheses. Example: x−9=0
Solving this, the result is 9.
This is the simplest way to solve this type of equation. You could also use the quadratic formula, substituting c as 0, but that would be more complicated. Either method is valid as long as you reach the correct solution.
How Can a Private Maths Tutor Help You with Complex Maths Equations?
Maths is a subject that can become increasingly complex as you advance through higher grades at school, with each year introducing more difficult concepts. This is why having a solid foundation is crucial. If you find it challenging to establish that foundation on your own, private maths tutors are experts in breaking down subjects into smaller, more manageable chunks, helping you understand the material better.
The most important benefit of having a private maths tutor is that you can have maths lessons in whatever format you prefer. You can find an in person or online private maths tutors, or you can find a GCSE or A-level tutor if you think you need help with exam prep. It's totally up to you since the lessons will be personalised to your needs.
Related articles:
- How to Solve Mathematical Equations Step by Step
- How to Solve Higher-Order Equations Easily
- How to Solve Quadratic Equations in the Simplest Way


