What are Newton´s Laws? How do you use them?
Newton's Laws provide the framework that explains how objects move, why they stay still, and the intricate forces that govern our physical world. Join me, a maths and physics tutor, as we unravel the mysteries of the universe and gain a deeper understanding of the science that shapes our daily lives.
Now it is important to understand Newton has had many discoveries, laws and theorems in his lifetime. But for the sake of this article we are going to cover his major 3 laws of motion.
Now first things first, what is Newton's 1st Law?
"An object will remain at rest or stay in motion unless compelled to change its state due to an external force"
This is also called the Principle of Inertia, now there are many ways to describe inertia but one could call it a physical object's reluctance to a change in its motion.
This can be seen more mathematically in his second law though, but for now let's focus on this first one, it basically means if we had a rock on the ground, it will stay on the ground unless someone pushes or pulls it. Why? Because there is no external force! Meaning that there is no Resultant Force, gravity acts on the rock causing it to have a weight force towards the centre of the Earth and then there is an equal and opposite force (see Newton's third law) that means it has balanced forces!
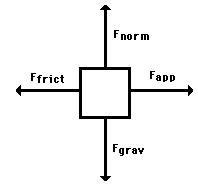
Now what can we take away from this for use in calculations and questions?
A lot actually! Or maybe not a lot, but possibly the key amount necessary to start calculations!
So another way to see this is, if an object is at rest we can use Newton's First law as justification to say there is no resultant force acting on it. Now this is SUPER important, it means, like in the above diagram, that all the forces acting on our rested object are equal in magnitude and opposite, thus they all cancel out.
The same is true for an object moving at constant velocity, now some of the clever ones will say: "Oh but, how can the same be true for a moving object? Won't it slow down eventually?" and you're not wrong, but in reality there are many forces at play and really nothing will truly be at rest or constant velocity, but for your exams there will be things at rest and in constant velocity, why? Because we model them that way for the convenience of using these laws. Im getting sidetracked... the main takeaway is if there is an object moving at constant velocity, it means it has no resultant force this will, again, be clarified in the second law.
Great, Now what's Newton's 2nd Law?
"The acceleration of an object, as produced by a net force, is directly proportional to the net force in the same direction as that of the net force and is inversely proportional to the object's mass."
Now this is probably the most important law, any physics and even maths syllabus out there will make use of this in their mechanics modules in some way or another. So... what is it?
Newton's 2nd law is often abbreviated as F = ma and famous equation as it is, a lot of students look at that and take it at face value, only to take A level (High School) physics later and learn they had no idea what the equation they were using even meant! That being said it isn't wrong either, but let's clarify a few things:
What does proportionality mean?
Well... for conciseness I will sum it up to your maths teacher to tell you, (im kidding). Ok so truly this means for one variable to increase or decrease, with another, in a specific ratio. This ratio is usually given by a constant, in the case of our equation, this will be m, the mass of our object in its system. (But could also be a or F, but usually they are the variables that change) So let's do a little rearranging on this formula;
a = F/m, a = (1/m)F
Now, as can be seen, there are a few key points here, when mass increases for a constant force acting on an object, there acceleration will decrease, this reinforces the concept of inertia. For a bigger (more massive) object it is more reluctant to move, or in another way of saying the acceleration is lower for the same force exerted. This shows that the accleration is inversely proportional to mass and directly proportional to force, since using the equation, if force increases for the same mass then accelration also increases!
What are variables actually indicating?

This diagram basically outlines a situation for us, but we know what a Force and mass is, but what is acceleration? Well it is basically when an object has a change in velocity, we measure it as the change in velocity per unit time (m/s^2). Keep in mind the Force used in this law is always the net or resultant force, it is absolutely essential you remember this!
But since im also catering this for A level students, we can call acceleration, dv/dt, the derivative of velocity with respect to time. (Fun fact: Newton had a large role in inventing calculus, likely for the purposes of utilising these laws.)
In my interest of helping your understanding we can rewrite F = ma into;
F = mΔv/Δt , F = m(Δv/Δt) , F = m(dv/dt)
Δ - means "change in (some variable)"
See anything familiar? No? Well we can see mΔv which can be written as ΔP, where P is momentum and ΔP is the impulse, and thus we have come up with a more precise way of writing Newton's 2nd law:
"The force exerted on an object is equal to the rate of change in its momentum as a result"
This is immensely useful, it puts our second law which has the closest relation to motion in a graphical context. So let's say you're given a velocity-time or momentum-time or, if it's detailed, even a displacement-time graph. You can use this modified version of Newton's second law to make short work of what may initially seem like a daunting task.
For those who aren't familiar with calculus, assuming you are aware of basic graphs y-x, we call dy/dx the same as Δy/Δx this is due to the definition of dy/dx. A small change in y: dy, caused by a small change in x: dx, is represented as that ratio. (Also known as the gradient of a graph)
For reference, this is the graph I mean:

Takeaways for Newton's 2nd Law:
Only ever use F = ma or * F = dP/dt, to solve for a or m, when F is a resultant force. If given a graph look at the axis and decide how you can use the principals of how momentum changes with time, to answer questions. Truly this usage of Newton's law can only be truly refined in the field (practice questions), it's something you must understand both in concept and in practical use.
* dP/dt is just differential notation for the rate of change of momentum.
Newton's 3rd Law
"For every action, there is an equal but opposite reaction."
Probably the simplest law out of all 3 laws of motion and likely why you'll hear it so much in media. That being said, there are a few things you have to take away from this;
- Any force acting on an object will have a reactionary force (the one that pushes back).
- The reaction force has opposite vector direction but has the same magnitude.
"Hold on a moment, that's a bit confusing, which force is acting on what and where?" - is the question that, ironically, no one asks usually. But I will answer it anyway;
In reality, for a pair of forces to be called a "Newton's 3rd law pair" they must act on different objects. The reason could come down to accounting for all forces, for example if you left a mug on the table and mug is being pulled downward towards the Earth by it's weight, in a similar way the mug is also pulling the Earth toward itself with an equal but opposite gravitational force due to its own gravity. These opposing forces would be Newton's third law pairs but not the reaction force of the table on the mug, because the table is pushing the mug back and gravity is pulling the mug against the table. Meaning the reaction force and the weight force are both acting on the mug only.
Ofcourse, this may sound absolutely absurd, how could it be that the entire Earth is being pulled by a mug? This is can be de-mystified in a few visualisations or even using some formulae. Let's take it that the mug is pulling the Earth toward it, that means both the Earth and the mug are experiencing the same magnitude of force, but remember F = ma and when we use it with the principle of inertia something very interesting happens;
Given m = mass of mug , M = mass of the Earth , F₉ = The force of gravity , g = acceleration of mug , a = acceleration of Earth
F₉ = mg = Ma
given we know M = (2x10^25)m (Yes, it would take that many mugs to have the mass of Earth)
mg = (2x10^25)ma
a = g/(2x10^25)
a ≈ 4.905x10^-25 ms^-2 (given standard values for an average mug and the Earth)
As the above calculation exemplifies, due to the Earth's massive inertia, it's acceleration due to the mug pulling it back is practically infinitely smaller than the effect of the Earth pulling on the mug.
So key takeaway for the 3rd law is to watch out for what objects the forces are acting on! And thus we will rewrite the common saying into something more specific;
Newton's 3rd Law : "For an object X, which experiences a force caused by an object Y, object X will exert a equal but opposite force on object Y"
After reading this article you should have an improved understanding of Newton's Laws of motion and possibly a few of the quirks they present in your upcoming exams!
Or at the very least I hoped you enjoyed reading!
If you need private tuition for maths or science lessons, I am a private tutor offering classes in these areas. Feel free to reach out to me for more information.

