8÷2(2+2)=? Many get this clickbait question wrong. How to get bracketed order of operations right.

   You have probably seen a question like 8÷2(2+2) going around on socials, and much debate about the answer. In fact, it's precisely because people hotly debate it that it gets posted - it's clickbait, designed to get people engaged (on a particular website or whatever). Many people claim it's ambiguous, and yet it's not actually. Year 7-8 Maths textbooks are quite clear about how to do it. I'm going to take you through how to get it right, how people get it wrong ("but...." - no buts), and share a few memes along the way as well... that you can use the next time you see people getting it wrong. 😉 The two most important take-aways are...
#MathsIsNeverAmbiguous

#DontForgetDistribution

   The 3 Mathematical concepts we shall discuss are order of operations, distribution, and terms - it's usually in one of these 3 areas where people go wrong. I cover these 3 areas in depth, so feel free to scroll down to the summary at the end and come back to anything you want to read more about. Let's begin...

   First, try it yourself - take note of what steps you follow to get the answer. Following the right steps is the key to getting the right answer. you will commonly see 2 answers - 1, and 16. You will also see people who say 16 say "the question is ambiguous - there are 2 valid answers". Nope, #MathsIsNeverAmbiguous, there is one answer, and it's 1. People who get 16 have missed one or more rules of Maths. Let's start with talking about one of those rules - order of operations...

ORDER OF OPERATIONS MNEMONICS

People - sometimes even a majority of people - can often forget the rules of Maths, as we can see in this meme...

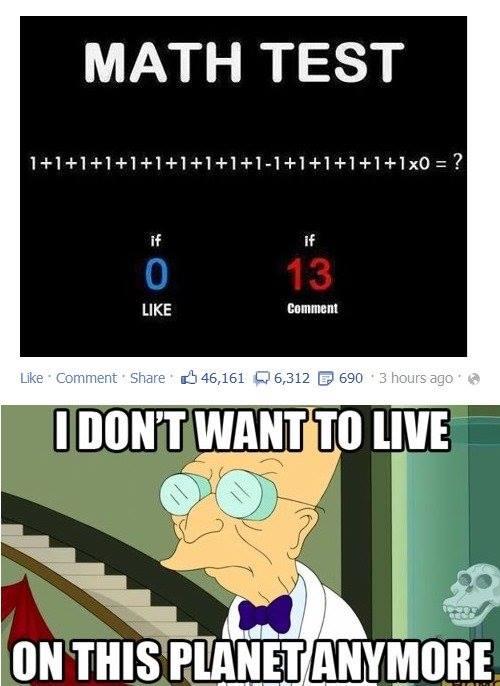
   So sometimes we have mnemonics - a way to remember something - to help us remember the rules, and this is the case for order of operations. There are different mnemonics used in different cultures - here are all the ones that I'm aware of...
BEDMAS - Brackets Exponents Division Multiplication Addition Subtraction
BIDMAS - Brackets Indices Division Multiplication Addition Subtraction
BODMAS - Brackets Order of Division Multiplication Addition Subtraction

PEMDAS - Parentheses Exponents Multiplication Division Addition Subtraction

   The first 3 are basically the same, except for the second letter, which are all just different names used for the same thing to remember, that being powers (exponent, index, order of). I think the first is the easiest to remember, cos you just imagine a big 4-poster bed - it's a BED with a lot of MASs. 🙂

   The last one is predominant in America, and so much harder to remember that they made up a sentence just to remember the mnemonic by(!) - Please Excuse My Dear Aunt Sally (note: always good to make mnemonics out of actual words if you can - much easier to remember - hence I prefer the first or second one, though the first one is best, cos 4-poster bed. 🙂 Having an image to associate with something also makes it easier to remember).

   You'll notice a difference between the last one and the first three, that being MD vs. DM, and this leads some to claim, incorrectly, that the rules depend on where you learnt them (divsion before multiplication, or multiplication before division), but the mnemonics aren't the rules - all the menomics are simply ways to remember the rules. Here is a graphic of the actual rules...

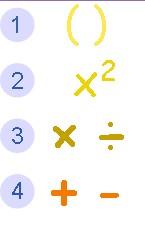
   3rd in the order (not 3rd and 4th) is multiplication AND division (followed by addition AND subtraction) - it doesn't actually matter which order you do multiplication and division, as long as you do them after exponents and before addition and subtraction. Note though that division itself needs to be done left-to-right.

APPLYING ORDER OF OPERATIONS

   This brings us to the first place where many people go wrong (which will be discussed more shortly) - exactly what "multiplication" means, particularly when it comes to the 2(2+2) part. Let me tell you that multiplication means literally any multiplication symbols, and there are NO multiplication symbols in this expression! In 8÷2(2+2) we only have division, brackets, and addition, and we always do brackets first. Anyone who does the division before solving the brackets (which many people do) has just violated the order of operations rules. The reason they do that, they argue, is that 2(2+2)=2*(2+2), and further (as per our previous point), they think you have to do division before multiplcation (which is incorrect in itself anyway). But this isn't actually multiplication, it's distribution, which brings us to...

THE DISTRIBUTIVE LAW - #DontForgetDistribution

   The Distributive Law in symbols is a(b+c)=(ab+ac), and is a subest of the topic expanding brackets (and in order of operations we have to do brackets first, so therefore we have to apply the Distributive Law). In a(b+c), "a" is known as a co-efficient of the bracketed term (we shall be talking more about terms shortly). Here are several textbook references about expanding brackets (and note the use of the words "must" and "everything" in the first one, and the use of the word "first" in the second one) - you can see which textbook it has come from in the top-left of the PDF...

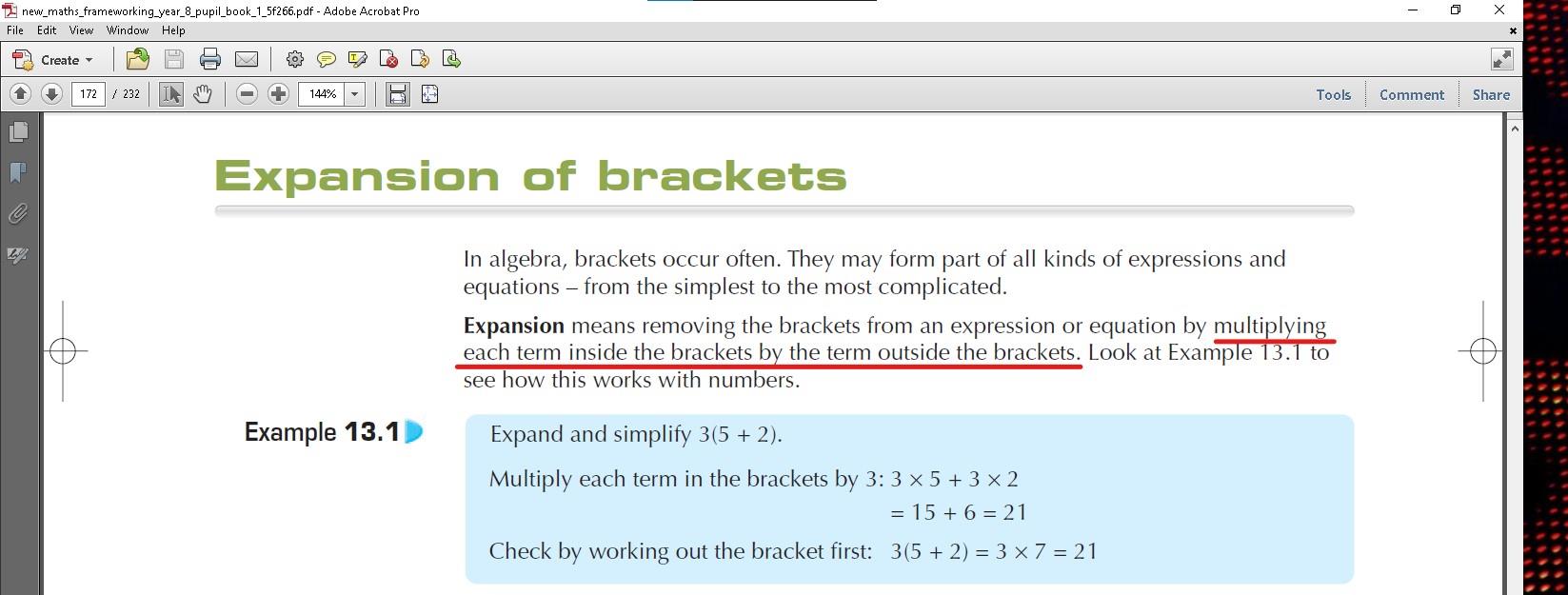
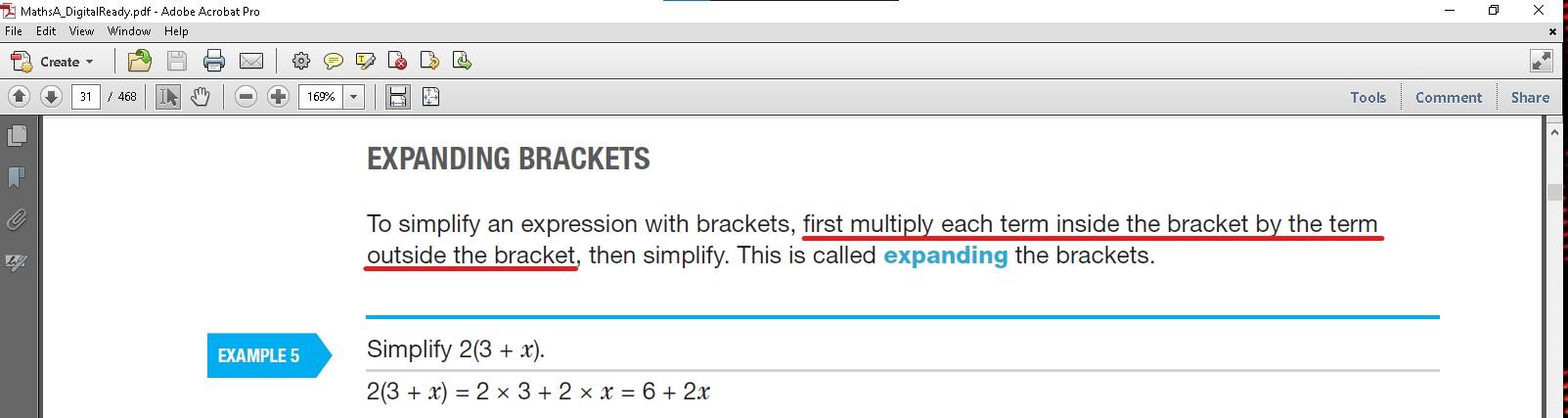
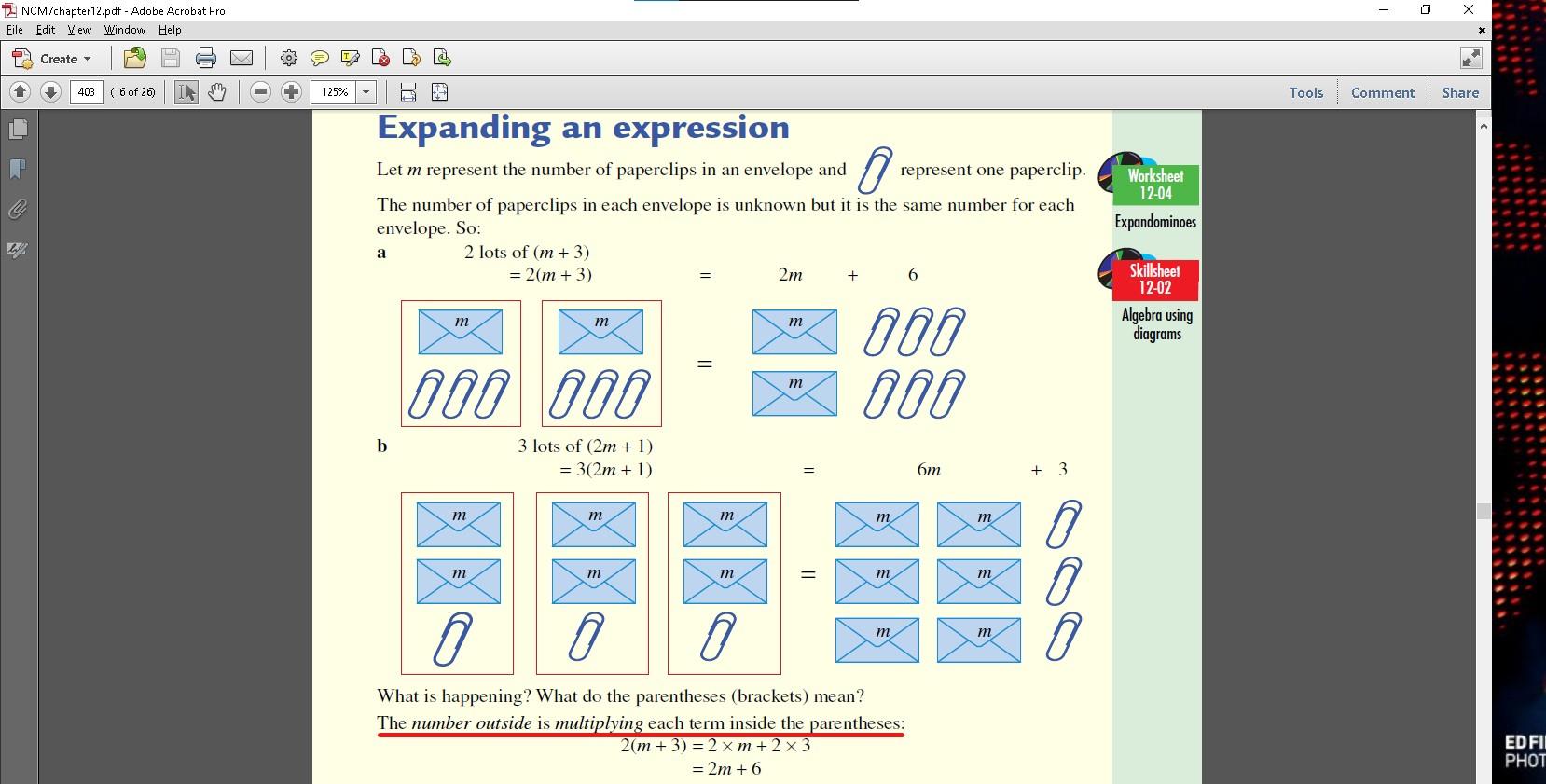
   ...and I have even more (I am a Maths teacher after all). 🙂 

   When we do a(b+c)=(ab+ac), we say that we have distributed a over b+c. So we can see here that Year 7-8 Maths textbooks all say the same thing - for any bracketed term which has a co-efficient, we must distribute that co-efficient over everything that is inside the brackets first. Further, in order of operations, we must do brackets first, which therefore means if there is any bracketed term we must expand brackets/distribute first. And so, this means when we have 8÷2(2+2), that means we must solve 2(2+2) first, before we do the division, otherwise we are violating order of operations rules. #DontForgetDistribution.

   A common objection I have heard at this point is "it means do what is inside the brackets". Well, that is what you are taught in primary school, when there are no co-efficients, but in high school you are introduced to bracketed expressions that have co-efficients, and corrspondingly the Distributive Law ("law" because you must do it, always). I find it interesting though that so many people remember a rule from primary school, and not what it was superseded by in high school - with high school being more recent you would think they would more likely remeber that - I guess a lot of students had primary school teachers who made a big impact on them? Not sure, but in any case that was most definitely only applicable when there were no co-efficients, or to be more precise a co-efficient which isn't 1. e.g. in ax(c+d), the (c+d) really has a co-efficient of 1, but we don't write it. i.e. ax(c+d) written out in full is actually ax1(c+d). We're distributing the 1, but of course when you multiply something by 1 you end up the same thing that you started with, hence it's unnecessary to write a co-efficient of 1, and Mathematicians don't like writing out un-necessary things. 😉 We keep it concise. So no, it's not "inside the brackets" first, it's brackets first (which includes any non-1 co-efficient).

   Before I move on, there's another way you can look at it (speaking of Mathematicians writing things as concisely as possible)...

   You are possibly familiar with expanding brackets for quadratic expressions. i.e. (a+b)(c+d)=(ac+ad+bc+bd). Well, when we have a single co-efficient, as opposed to another set of brackets, we could still write that in brackets! i.e. (a)(b+c). Would people still argue that we don't multiply (b+c) by a in this case? And yet this is the same expression, just without a in brackets... because Mathematicians don't like to write out things which are un-necessary! In fact the full expression would be written as 1(a)(b+c), but we leave out a co-efficient of 1, and we leave out brackets if there's only a single term inside it anyway.

   Lastly, before moving onto Terms (the other tripping point for some people), the reason the Distributive Law exists is that it's the opposite operation to factorising. In other words, if person A wants to factorise an expression, then we need to make sure that if person B wants to simplify it again, they get the same expression that person A started with, thus, we must follow the Distributive Law. If they don't, then they can end up with a different expression than what was started with. An example...

   Let's say I start with 1. What's another way I can get to 1? Well, 8÷8 is equal to 1, so that's another way I can write it. And, well, 8 has some factors, so let's factorise that second 8 - let's start with 2. 8 is 2x4, so let's rewrite that as 8÷2(4). And 4 is 2+2, so let's write 8÷2(2+2). And now, if we've written that, we must have sufficient rules in Maths to make sure anyone who wants to re-simplify that ends up with 1, and since the 2(2+2) is 8 in a factorised form, we need to make sure that gets simplified to 8, and so we have the Distributive Law (and order of operations), which makes sure that indeed we do simplify 2(2+2) before we do anything else.

   So bearing in mind that in a(b+c) we have to dstribute the "a", because it's a co-efficient, and there's no multiplication symbols involved, I made this meme to summarise all of what I've just discussed...

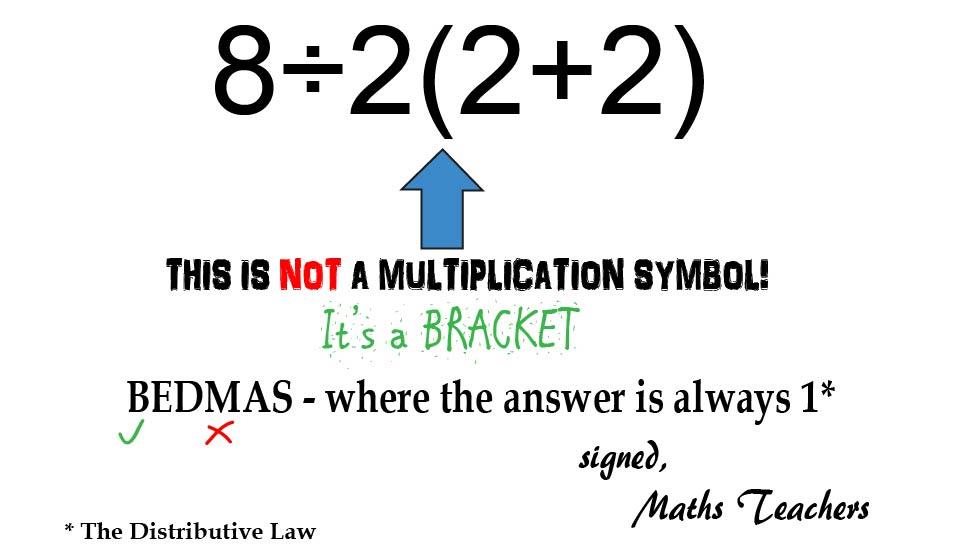
   Lastly...

TERMS

   Another thing that trips people up is not understanding Terms. An example of this, which also shows another example of things being written more concisely, is 2a=(2xa). Terms are separated by operators and joined by brackets, so if we intend 2xa to be treated as a single term - since it's currently 2 terms when written that way (a 2 and an a separated by a x) - we can indicate that by putting it in brackets, (2xa), or we can do it the way Matmaticians invented to write it more concisely, which is to leave out the multiplication sign, and just write it as 2a, hence 2a=(2xa). Getting back to our example, 2+2 is 2 terms (two 2's separated by a plus), (2+2) is one term - joined by brackets - and 2(2+2) is also 1 term joined by brackets, because the first 2 is a co-efficient of the bracketed term. We could write it as (2x(2+2)), but Mathematicians have invented this more concise way of writing it, which is 2(2+2). And to distinguish this second expression as being different, we say that as "2 outside of 2 plus 2", as opposed to "2 times 2 plus 2". "outside of" means it is a co-efficient of what follows inside the brackets. "2 times 2 plus 2" is 2 terms (2 and (2+2)), but "2 outside of 2 plus 2" is one term (2(2+2)). And, to re-iterate the previous point, when we have 2(2+2) there is no multiplication symbol, just a co-efficient that needs to be distributed over the brackets - there is just "2 outside of 2 plus 2".

   The common mistake I have seen people make here (probably the most common mistake of them all actually) is to say "well 2(2+2)=2*(2+2)". No, it's not. Can you see why? It's because you took 1 term and broke it up into 2 terms, and in the context of our original example, that would change the answer(!) - 8÷2(2+2)=8÷(4+4)=8÷8=1, but 8÷2x(2+2)=8÷2x4=4x4=16! THAT is why Terms and the Distributive Law matter!

   So again I made a meme for that...

..and then I made another meme using that meme I just made with one of the textbook references...

You didn't mention "implicit multiplication"?

No, because that's not actually a mathematical term. When I've seen people use that, what they've actually been talking about is The Distributive Law and/or Terms, and those are the correct mathematical terms for those things. No Mathematician talks about "implicit multiplication", only people who kindly vaguely remember the rules but not what they were actually called.

SUMMARY

Order of operations - BEDMAS - Brackets Exponents Division Multiplication Addition Subtraction, and don't forget the mnemonic isn't the rules! It's just a way to remember the rules - Brackets, then Exponents, then Division and Multiplication (division left-to-right), and finally Addition and Subtraction.

The Distributive Law - a(b+c)=(ab+ac) and this is the first step in solving brackets, and brackets is always first in order of operations, so if there is a bracketed term then the first thing we have to do is expand (and simplify) the brackets. #DontForgetDistribution

Terms - Terms are spearated by operators and joined by brackets. i.e. 2(2+2) is a single term, with a co-efficient of 2, and similarly 2a is a single term, because there's no operator separating the 2 and the a.

#MathsIsNeverAmbiguous

Thanks for reading. I hope you won't get sucked into any clickbait "Maths is ambiguous" debates (unless you're going to set them straight of course! 😉 ). Contact me if you'd like some online tutoring (in Maths or Computer Science). 😀